激活函数

为什么要用激活函数？

如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。 如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

常用的激活函数

Sigmoid：用于二分类神经网络输出

sigmoid函数也叫 Logistic 函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。

函数表达式：

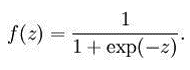
sigmoid的导数：

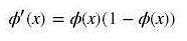
sigmoid缺点：

1. 指数运算计算量大，反向传播求误差梯度时，求导涉及除法。
2. 反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练
3. Sigmoids函数饱和且kill掉梯度。
4. Sigmoids函数收敛缓慢。函数输出不是以0为中心的，这样会使权重更新效率降低。

解释为何会出现梯度消失：

sigmoid导数图如下所示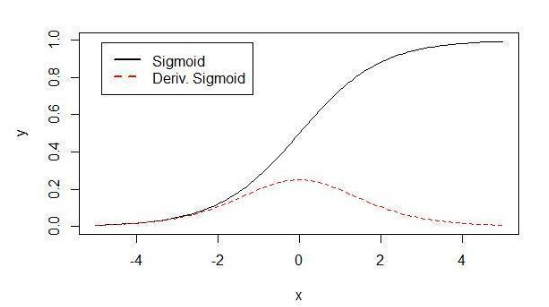： 由图可知，导数从 0 开始很快就又趋近于 0 了，易造成“梯度消失”现象。 由于在后向传递过程中，sigmoid向下传导的梯度包含了一个f’(x) 因子(sigmoid关于输入的导数)，因此一旦输入落入饱和区，f’(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说，sigmoid 网络在 5 层之内就会产生梯度消失现象。

Tanh

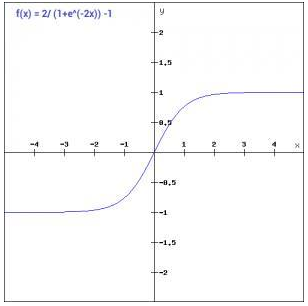
函数与其导数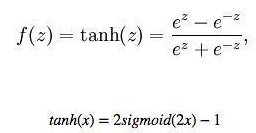： 也称为双切正切函数，取值范围为[-1,1]。

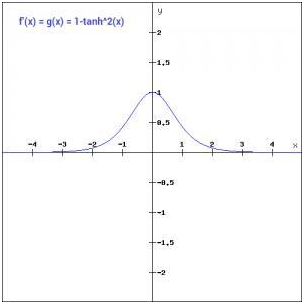
函数与导数的函数图：

特点：

tanh在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果。

和sigmod函数的曲线是比较相近的，首先相同的是，这两个函数在输入很大或是很小的时候，输出都几乎平滑，梯度很小，不利于权重更新；

不同的是输出区间，tanh的输出区间是在(-1,1)之间，而且整个函数是以0为中心的，这个特点比sigmod的好。

ReLu：Rectified Linear Unit

表达式：

f(x) = max(0, x)

ReLu特点：

输入信号 0 的情况下，输出等于输入

ReLu 的优点：

1. 在输入为正数的时候，不存在梯度饱和问题。
2. 计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。（sigmod和tanh要计算指数，计算速度会比较慢）

ReLu 的缺点：

训练的时候很”脆弱”，很容易就”die”了。例如，一个非常大的梯度流过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了，那么这个神经元的梯度就永远都会是 0。 如果 learning rate 很大，那么很有可能网络中的 40% 的神经元都”dead”了。

1. 当输入是负数的时候，ReLU是完全不被激活的，这就表明一旦输入到了负数，ReLU就会死掉。这样在前向传播过程中，还不算什么问题，有的区域是敏感的，有的是不敏感的。但是到了反向传播过程中，输入负数，梯度就会完全到0，这个和sigmod函数、tanh函数有一样的问题。
2. 我们发现ReLU函数的输出要么是0，要么是正数，这也就是说，ReLU函数也不是以0为中心的函数。

改进函数：Leaky-ReLU、P-ReLU、R-ReLU

Softmax：用于多分类神经网络输出

函数表达式:

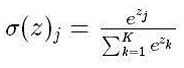
输入映射为0-1之间的实数，并且归一化保证和为1。

为什么要取指数?

第一个原因是要模拟 max 的行为，所以要让大的更大。

第二个原因是需要一个可导的函数。

反向求导：

见网页