卷积
目录
2D卷积操作
我们用一个简单的例子来讲述如何计算卷积，然后，我们抽象出卷积层的一些重要概念和计算方法。
假设有一个（5，5）的图像，使用一个（3，3）的filter进行卷积，想得到一个（3，3）的feature map，如下所示：
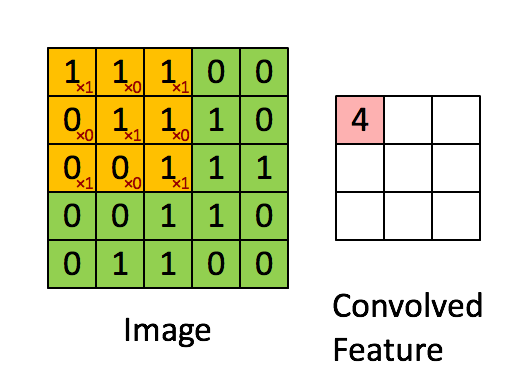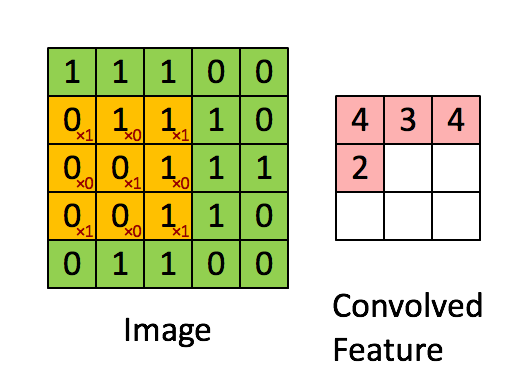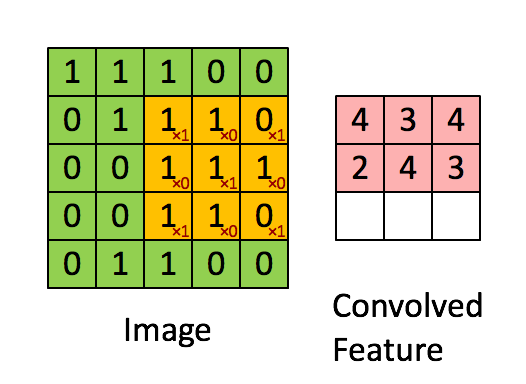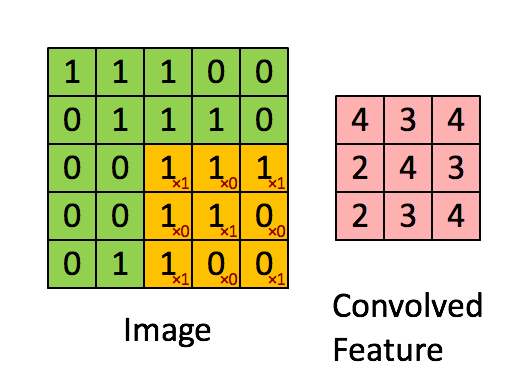Stride=1， padding=1的卷积如下图所示：
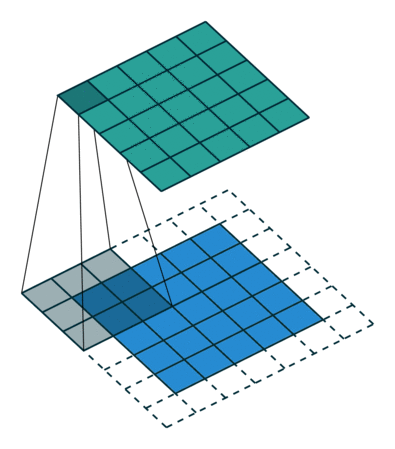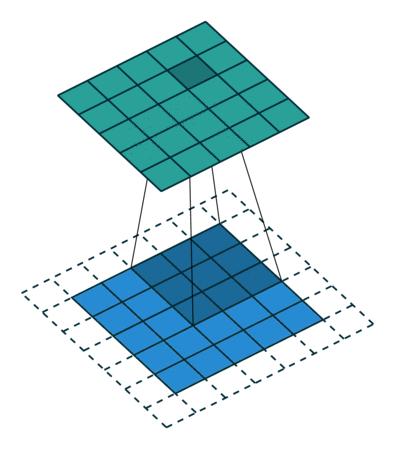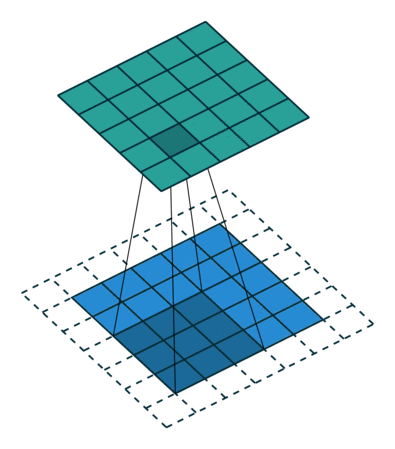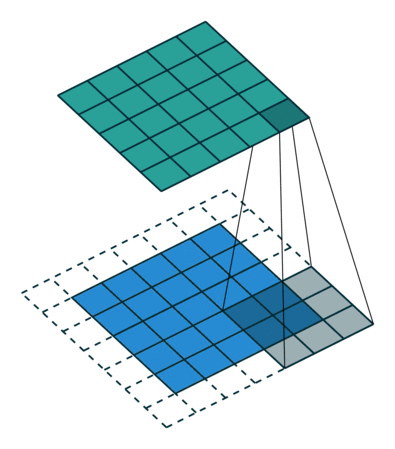由图中可以看到图像大小、步幅和卷积后的Feature Map大小是有关系的。
W2 = (W1 - F + 2P)/S + 1
H2 = (H1 - F + 2P)/S + 1
W是卷积前后图像的宽度；F是filter的宽度(即，kernel_size大小)；P是Zero Padding数量，Zero Padding是指在原始图像周围补几圈0，如果的值是1，那么就补1圈0；S是步幅；H是卷积前后的高度；
对于彩色图像三通道(RGB)的卷积过程如下图所示：
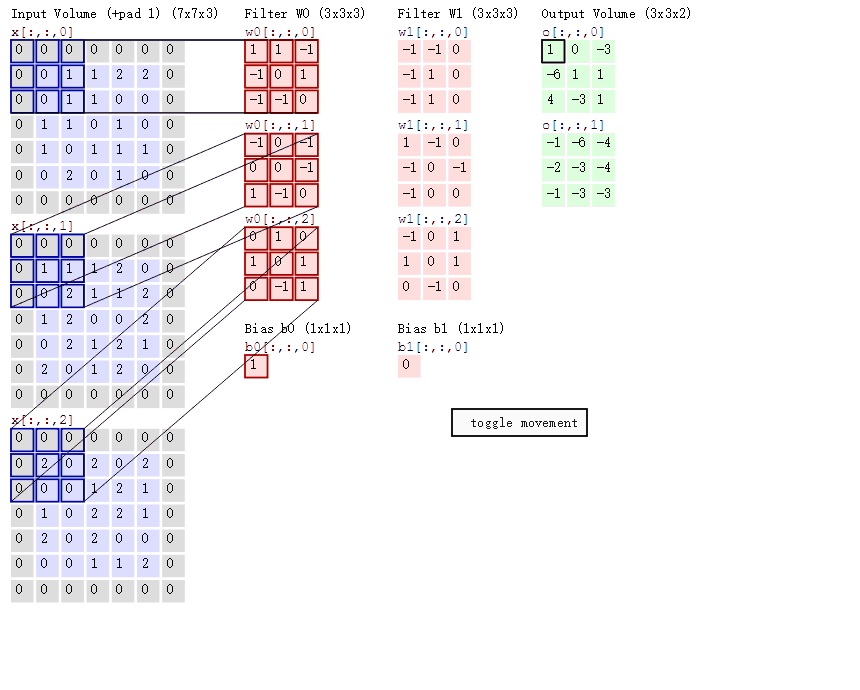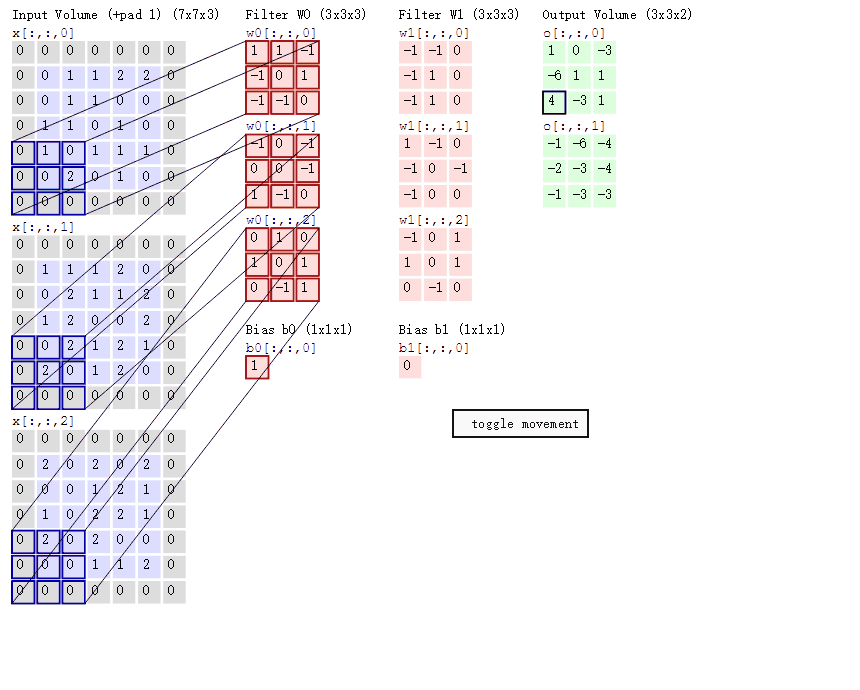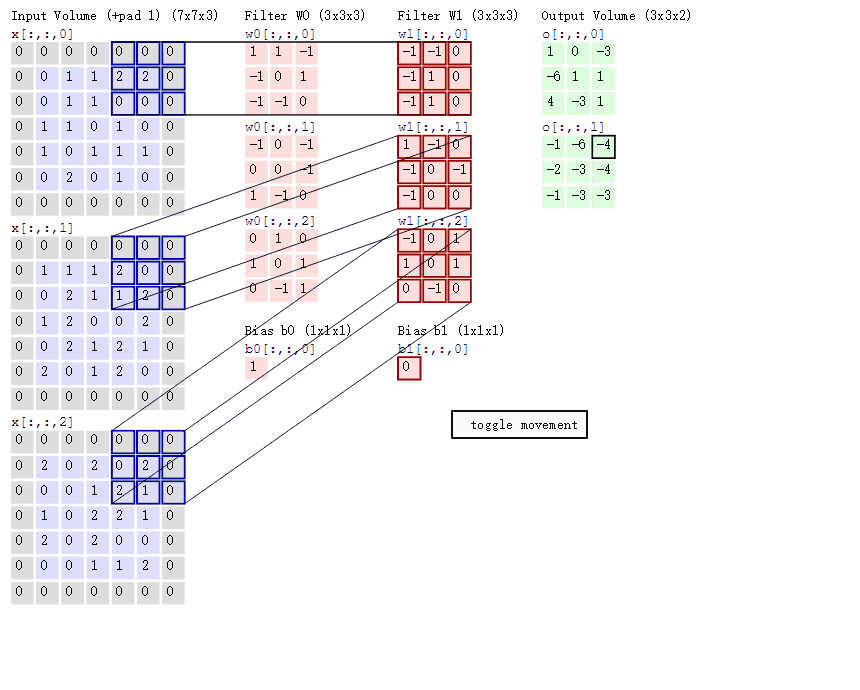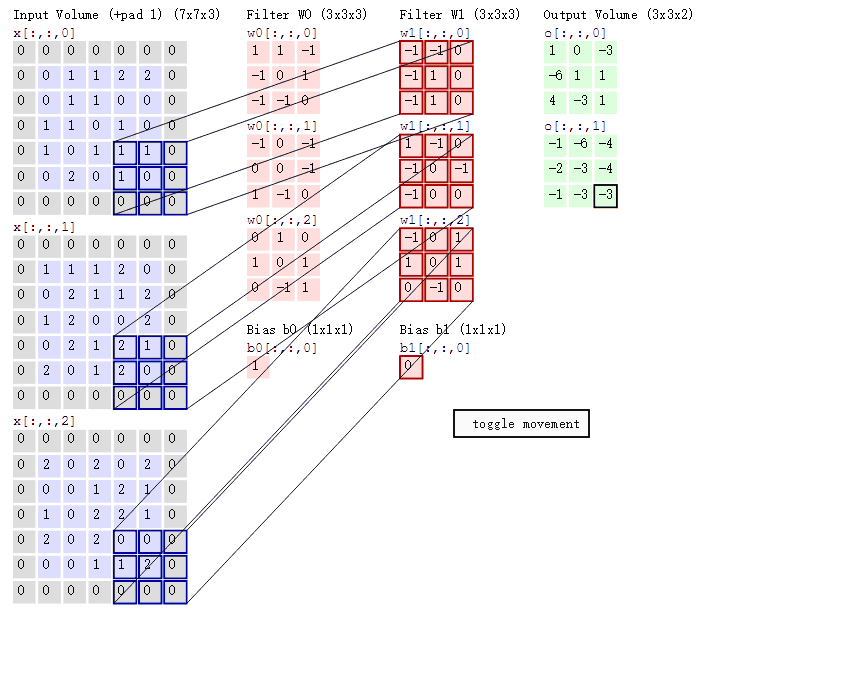
其他变形的卷积操作见博客
平铺卷积(tiled cnn)请见各种类型的卷积或者Tiled CNN
介绍
网络层参数计算
以LeNet网络架构为例：
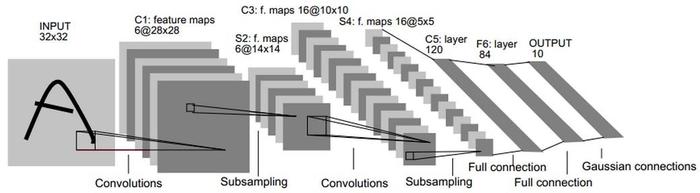
网络结构可训练参数个数和连接个数计算如下所示：
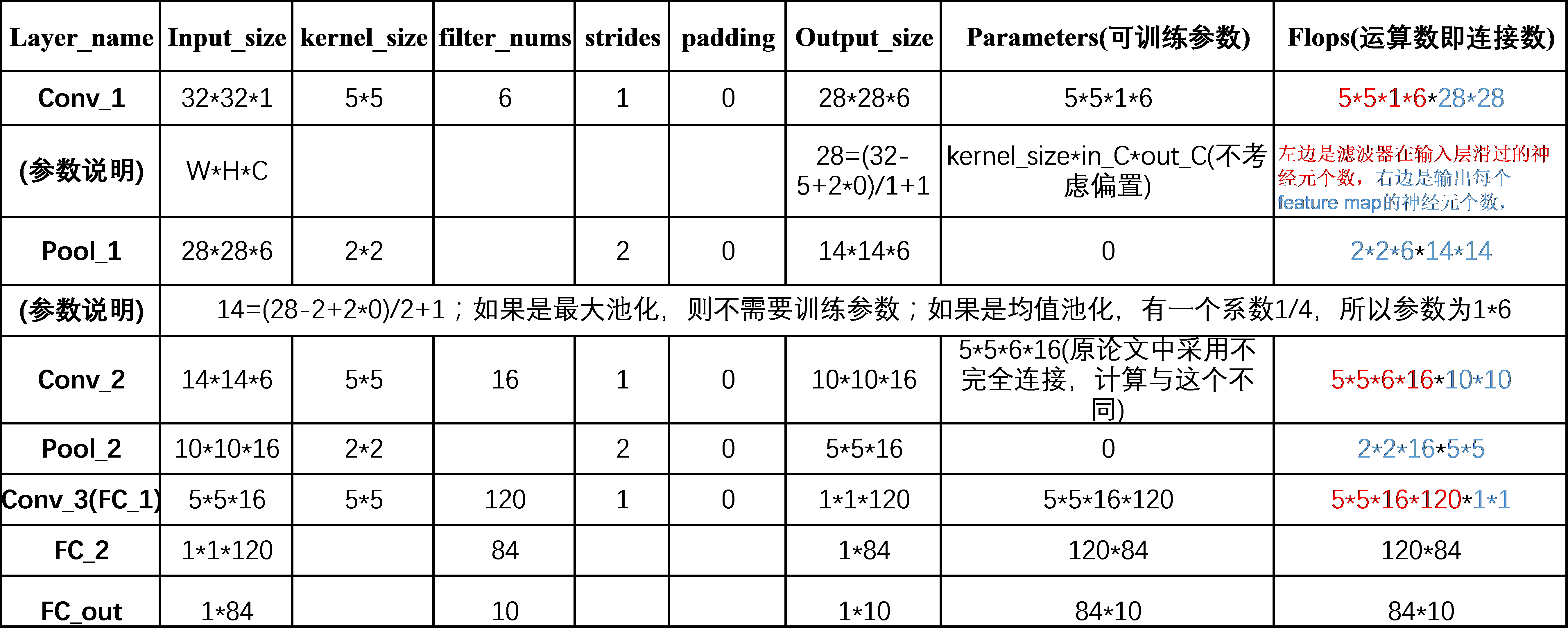
感受野参数计算如下：
在卷积神经网络中，感受野的定义是 卷积神经网络每一层输出的特征图（feature map）上的像素点在原始图像上映射的区域大小。如下图：
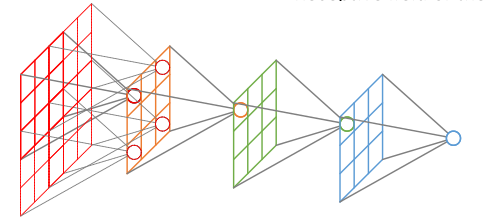
感受野计算时有下面的几个情况需要说明：
（1）第一层卷积层的输出特征图像素的感受野的大小等于滤波器的大小
（2）深层卷积层的感受野大小和它之前所有层的滤波器大小和步长有关系
（3）计算感受野大小时，忽略了图像边缘的影响，即不考虑padding的大小
关于感受野大小的计算采用top to down的方式， 即先计算最深层在前一层上的感受野，然后逐渐传递到第一层，使用的公式可以表示如下：
RF = 1 #待计算的feature map上的感受野大小
for layer in （top layer To down layer）:
RF = ((RF -1)* stride) + fsize
stride 表示卷积的步长； fsize表示卷积层滤波器的大小
代码实现见网页
常见分类网络的结构及参数计算见博客
CNN反向传播
反向传播过程见网页
补充3D卷积
1D卷积是对只有一个维度的时间序列提取特征，比如信号、股价、天气、文本等等。普通的2D卷积是提取的单张静态图像的空间特征，同神经网络结合之后在图像的分类、检测等任务上取得了很好的效果。但是对视频，即多帧图像就束手无策了，因为2D卷积没有考虑到图像之间的时间维度上的物体运动信息，即光流场。因此，为了能够对视频进行特征，以便用来分类等任务，就提出了3D卷积。
3D卷积是通过堆叠多个连续的图片组成一个立方体，然后在立方体中运用3D卷积核。在这个结构中，卷积层中每一个特征map都会与上一层中多个邻近的连续帧相连，因此捕捉空间/时间上的变化信息。例如下面右图，一个卷积map的某一位置的值是通过卷积上一层的三个连续的帧的同一个位置的局部感受野得到的。
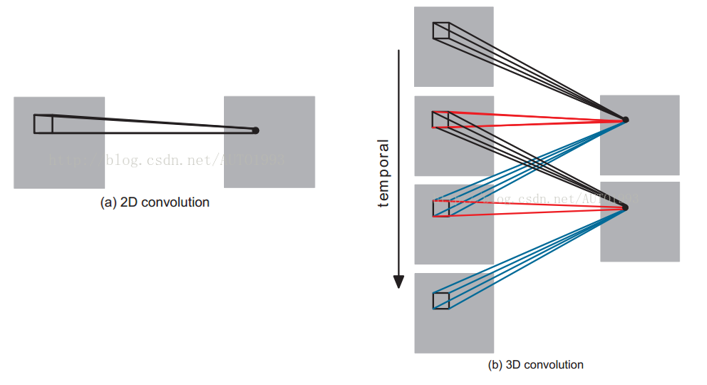以立体展示对比更直观：
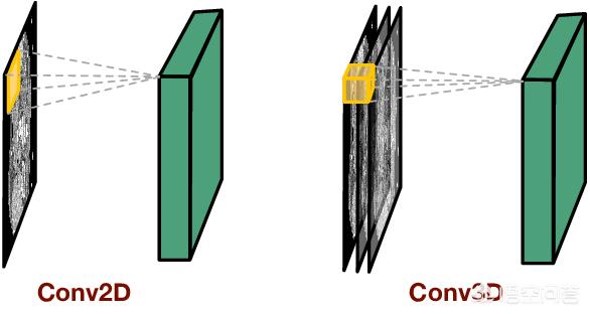
注意：3D卷积核只能从cube中提取一种类型的特征，因为在整个cube中卷积核的权值都是一样的，也就是共享权值，都是同一个卷积核（图中同一个颜色的连接线表示相同的权值）。我们可以采用多种卷积核，以提取多种特征。
