L1正则化

L1范数是指向量中各个元素绝对值之和，也有个美称叫“稀疏规则算子”（Lasso regularization）

(任何的规则化算子，如果他在Wi=0的地方不可微，并且可以分解为一个“求和”的形式，那么这个规则化算子就可以实现稀疏。)

既然L0可以实现稀疏，为什么不用L0，而要用L1呢？

个人理解一是因为L0范数很难优化求解（NP难问题），二是L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。

L1范数和L0范数可以实现稀疏，L1因具有比L0更好的优化求解特性而被广泛应用。

L2正则化

L2范数: 指向量各元素的平方和然后求平方根。它也不逊于L1范数，它有两个美称，在回归里面，有人把有它的回归叫岭回归（Ridge Regression），有人也叫它“权值衰减weight decay”。强大功效是改善机器学习里面一个非常重要的问题：过拟合。

我们让L2范数的规则项W模的平方最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0。而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。参数越多，模型越复杂，而越复杂的模型越容易过拟合。

我们让L2范数的规则项W模的平方2最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0。而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。参数越多，模型越复杂，而越复杂的模型越容易过拟合。

L1与L2的对比

L1-norm(范数)，也叫作最小绝对偏差（leastabsolute deviations, LAD），最小绝对误差（least absolute errors，LAE）.

L2-norm(范数)也称为最小均方(least squares)，它是最小化目标值yi和估计值f(xi)平方和。

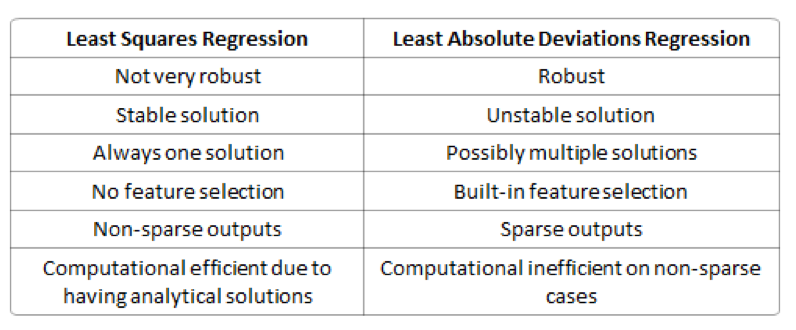
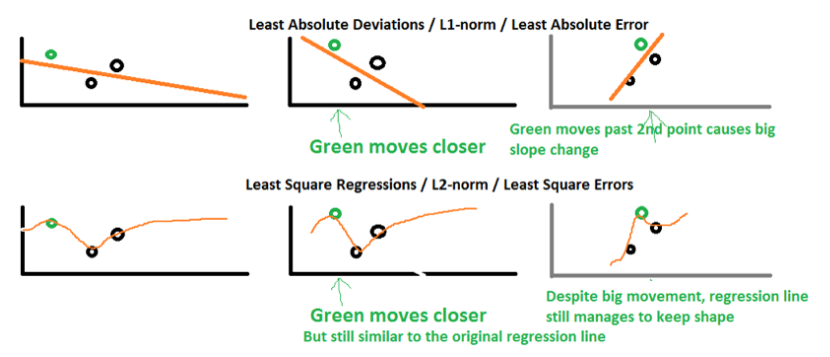
鲁棒性（Robustness）：最小绝对值偏差的方法应用领域很广，相比最小均方的方法，它的鲁棒性更好，LAD能对数据中的异常点有很好的抗干扰能力，异常点可以安全的和高效的忽略，这对研究帮助很大。如果异常值对研究很重要，最小均方误差则是更好的选择。

对于L2-norm，由于是均方误差，如果误差>1的话，那么平方后，相比L-norm而言，误差就会被放大很多。因此模型会对样例更敏感。如果样例是一个异常值，模型会调整最小化异常值的情况，以牺牲其它更一般样例为代价，因为相比单个异常样例，那些一般的样例会得到更小的损失误差。

稳定性：LAD方法的不稳定属性意思是，对于一个书评调整的数据集，回归线可能会跳跃很大。这个方法对一些数据配置有连续的解决方法；可是，通过把数据集变小，LAD可以跳过一个有多个求解拓展区域的布局（one could “jump past” a configurationwhich has multiple solutions that span a region，这句翻译挺麻烦的，大家自己领会吧，我尽力了），再通过这个解决方案的区域后，LAD线有一个斜坡，可能和之前的线完全不同。相比较之下，最小均方解决方法是稳定的，对于任何晓得数据点的调整，回归线仅仅只稍微移动一下，回归参数就是数据的连续函数（continuousfunctions of the data）

计算效率（Computational efficiency）：L1-norm没有一个解析解（analytical solution），但是L2-nom有，这使得L2-norm可以被高效的计算。可是，L1-norm的解有稀疏的属性，它可以和稀疏算法一起用，这可以是计算更加高效。

稀疏性解释

来看看它们解的分布性：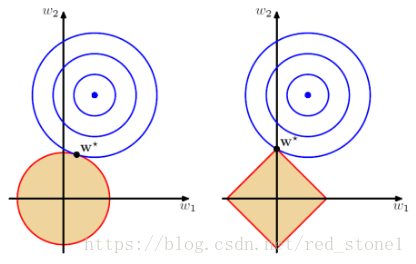

以二维情况讨论，上图左边是 L2 正则化，右边是 L1 正则化。从另一个方面来看，满足正则化条件，实际上是求解蓝色区域与黄色区域的交点，即同时满足限定条件和 Ein 最小化。对于 L2 来说，限定区域是圆，这样，得到的解 w1 或 w2 为 0 的概率很小，很大概率是非零的。

对于 L1 来说，限定区域是正方形，方形与蓝色区域相交的交点是顶点的概率很大，这从视觉和常识上来看是很容易理解的。也就是说，方形的凸点会更接近 Ein 最优解对应的 wlin 位置，而凸点处必有 w1 或 w2 为 0。这样，得到的解 w1 或 w2 为零的概率就很大了。所以，L1 正则化的解具有稀疏性。

扩展到高维，同样的道理，L2 的限定区域是平滑的，与中心点等距；而 L1 的限定区域是包含凸点的，尖锐的。这些凸点更接近 Ein 的最优解位置，而在这些凸点上，很多 wj 为 0。

（ 对于正则化参数，若λ 很小，容易造成过拟合。相反，若 λ 过大容易造成欠拟合。详细解释见网页）