常见评价指标
分类和回归对应的指标
| 学习分类 | 性能指标 |
|---|---|
| 分类 | Accuracy、precision、Recall、F1 Score、ROC Curve、PR Curve、AUC等 |
| 回归 | MAE、MSE等 |
分类
混淆矩阵
详细解释见维基百科Confusion matrix。该网页将混淆矩阵以及基于混淆矩阵拓展的多种指标的公式阐述的非常详细和清晰,如Precision,Recall/TPR,FPR,F1 score等等。
(查准率precision 和查全率recall 是一对矛盾的变量,P高R往往低;而R高P往往低,所以采用F1 score取两者的调和平均。)
P-R 曲线
以查准率P(presicion)为纵轴,查全率R(recall)为横轴。
示意图如下:
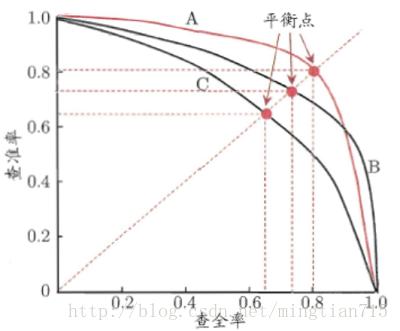
如何作图?
根据学习器的预测结果对样例排序,排在前面的是学习器认为“最可能”是正例的样本,后面的认为“最不可能”是正例的样本。按此顺序逐个把样本作为正例进行预测,即以当前点概率为划分阈值,前面判为正例,后面判为反例,计算当前的P和R。
举例:
若数据库有500条记录,其中50个相关(正样本),假设通过一个学习器后预测概率排序,以当前概率为阈值,返回了75个1,其中45个是真正的1。
则R = 45/50 = 0.9; P = 45/75 = 0.6;则当前点的坐标即为(0.9,0.6)。依次类推。。。
如果一个学习器的P-R曲线被另一个学习器的P-R曲线完全包住,则可断言后者的性能优于前者,例如上面的A和B优于学习器C,但是A和B的性能无法直接判断,但我们往往仍希望把学习器A和学习器B进行一个比较,我们可以根据曲线下方的面积大小来进行比较,但更常用的是平衡点或者是F1值。
平衡点(Break-Even Point,BEP)是查准率=查全率时的取值,如果这个值较大,则说明学习器的性能较好。但BEP还是过于简化了些,更常用的是F1度量。F1 = 2×P×R/(P+R),同样,F1值越大,我们可以认为该学习器的性能较好。
ROC曲线,全称是“受试者工作特征”(Receiver Operating Characteristic)曲线
以“真正例率”(True Positive Rate,TPR)为纵轴,“假正例率”(False Positive Rate, FPR)为横轴。
示意图如下:
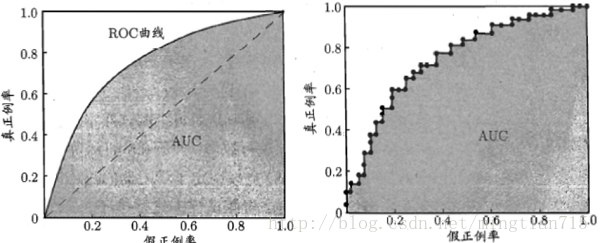 右图是基于有限样例绘制的ROC和AUC。
右图是基于有限样例绘制的ROC和AUC。
AUC曲线(Area Under ROC Curve):ROC曲线下的面积。AUC能很好地描述模型整体性能的高低
如何作图?
通PR曲线一样,给定m个正例,n个反例,根据学习器预测结果进行排序,先把分类阈值设为最大,使得所有例子均预测为反例,此时TPR和FPR均为0,在(0,0)处标记一个点,再将分类阈值依次设为每个样例的预测值,即依次将每个例子划分为正例。设前一个坐标为(x,y),若当前为真正例,对应标记点为(x,y+1/m),若当前为假正例,则标记点为(x+1/n,y),然后依次连接各点。
下面举个绘图例子:
有10个样例子,5个正例子,5个反例子。有两个学习器A,B,分别对10个例子进行预测,按照预测的值(这里就不具体列了)从高到低排序结果如下:
A:[反正正正反反正正反反]
B : [反正反反反正正正正反]
按照绘图过程,可以得到学习器对应的ROC曲线点
A:y:[0,0,0.2,0.4,0.6,0.6,0.6,0.8,1,1,1]
x:[0,0.2,0.2,0.2,0.2,0.4,0.6,0.6,0.6,0.8,1]
B:y:[0,0,0.2,0.2,0.2,0.2,0.4,0.6,0.8,1,1]
x:[0,0.2,0.2,0.4,0.6,0.8,0.8,0.8,0.8,0.8,1]
绘制曲线结果如下:
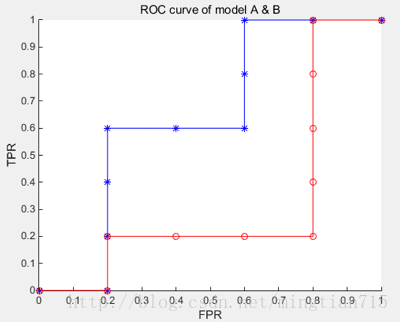
图中蓝色为学习器A的ROC曲线,其包含了B的曲线,说明它性能更优秀,这点从A,B对10个例子的排序结果显然是能看出来的,A中正例排序高的数目多于B。此外,如果两个曲线有交叉,则需要计算曲线围住的面积(AUC)来评价性能优劣。
K-S曲线、KS值
AUC只评价了模型的整体训练效果,并没有指出如何划分类别让预估的效果达到最好。 而KS也能达到相同的效果,还能给出最佳的划分阈值。
KS(Kolmogorov-Smirnov)评价指标:通过衡量好坏样本累计分布之间的差值,来评估模型的风险区分能力。好坏样本累计差异越大,KS指标越大,那么模型的风险区分能力越强。
K-S曲线如何作图?
K-S曲线,它和ROC曲线的画法异曲同工。首先把模型输出的概率从大到小排序,然后取10%的值(也就是概率值)作为阀值,同理把10%k(k=1,2,3,…,9)处的值作为阀值,计算出不同的FPR和TPR值,以10%k(k=1,2,3,…,9)为横坐标,分别以TPR和FPR的值为纵坐标,就可以画出两个曲线,这就是K-S曲线。
从K-S曲线就能衍生出KS值,KS=max(TPR-FPR),即是两条曲线之间的最大间隔距离。当(TPR-FPR)最大时,也就是ΔTPR-ΔFPR=0,对应的横轴取值,便是最佳阈值。这和ROC曲线上找最优阀值的条件ΔTPR=ΔFPR是一样的。从这点也可以看出,ROC曲线、K-S曲线、KS值的本质是相同的。
举例说明:
现假设有一个训练好的二分类器对10个正负样本(正例5个,负例5个)进行预测,得分从高到低排序得到的最好预测结果为[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],即5个正例均排在5个负例前面,正例排在负例前面的概率为100%。
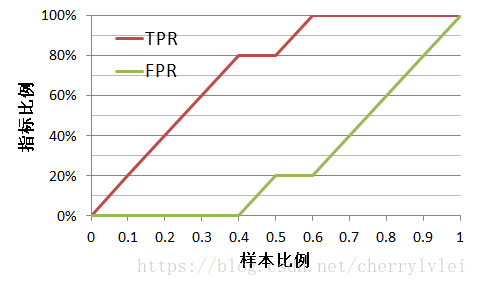
绘制其ks折线。首先,我们按照之前的描述方式,绘制TPR、FPR随着阈值(样本比例)变化的折线图,如下图所示:
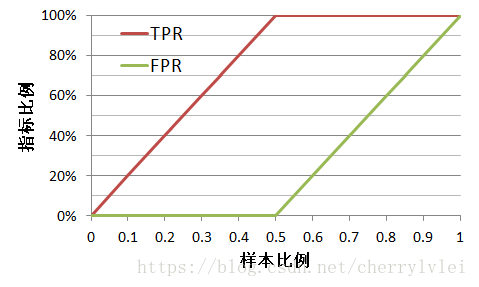 从上图我们可以知道,TPR提升最快而FPR提升最慢,的确说明了预测结果最好。然后,计算它们的差值,作ks折线图如下:
从上图我们可以知道,TPR提升最快而FPR提升最慢,的确说明了预测结果最好。然后,计算它们的差值,作ks折线图如下:
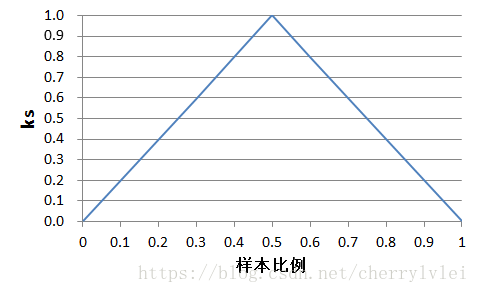 上图的ks值为1,最佳划分阈值是0.5,这是最理想的结果了。ks值域为[0, 1],一般情况下,ks值大于0.2就能判定模型是有效的。
上图的ks值为1,最佳划分阈值是0.5,这是最理想的结果了。ks值域为[0, 1],一般情况下,ks值大于0.2就能判定模型是有效的。
为了加深理解,我们稍微改变一下预测结果序列为[1, 1, 1, 1, 0, 1, 0, 0, 0, 0],看看ks值有何不同的变化。如下图所示:
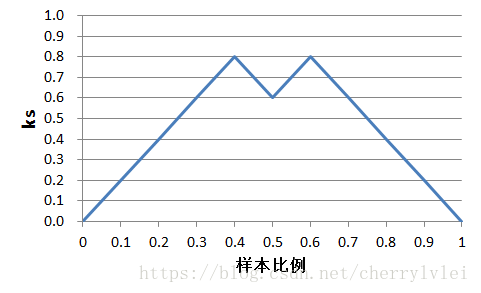 可知上图的ks值为0.8,最佳划分阈值为0.4或者0.6。
可知上图的ks值为0.8,最佳划分阈值为0.4或者0.6。
回归
平均绝对误差 MAE
平均绝对误差MAE(Mean Absolute Error)又被称为 l1 范数损失(l1-norm loss):
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_true,y_pred)
平均平方误差 MSE
平均平方误差 MSE(Mean Squared Error)又被称为 l2 范数损失(l2-norm loss):
from sklearn.metrics import mean_squared_error
mean_squared_error(y_true,y_pred)
更多指标及其指标所对应的公式详见网页
种草
pycm
安利一个基于混淆矩阵的各种评价指标计算非常齐全的python库:pycm,官方网站有安装方法,及github源码,文档介绍等等。。文档中每个指标的公式含义都有,写的非常详细。
sklearn
针对传统机器学习,强推使用python中的机器学习库-sklearn,可以直接调用集成的机器学习库函数,并有很多数据集、评价指标等,详细了解请见官网。






