欠/过拟合定义或产生的原因

一般在机器学习中，将学习器在训练集上的误差称为训练误差或者经验误差，在新样本上的误差称为泛化误差。显然我们希望得到泛化误差小的学习器，但是我们事先并不知道新样本，因此实际上往往努力使经验误差最小化。然而，当学习器将训练样本学的太好的时候，往往可能把训练样本自身的特点当做了潜在样本具有的一般性质。这样就会导致泛化性能下降，称之为过拟合，相反，欠拟合一般指对训练样本的一般性质尚未学习好，在训练集上仍然有较大的误差。

如何解决

欠拟合：

一般来说欠拟合更容易解决一些，例如增加模型的复杂度，增加决策树中的分支，增加神经网络中的训练次数等等。

过拟合：

一般认为过拟合是无法彻底避免的，因为机器学习面临的问题一般是np-hard,但是一个有效的解一定要在多项式内可以工作，所以会牺牲一些泛化能力。

过拟合的解决方案一般有增加样本数量，对样本进行降维，降低模型复杂度，利用先验知识(L1,L2正则化)，利用cross-validation，early stopping， 添加BN层、Dropout等等。

偏差与方差 与 欠/过拟合 的对应关系

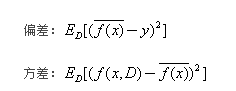
偏差和方差的计算公式: 泛化误差可以分解成偏差的平方加上方差加上噪声。

偏差度量了学习算法的期望预测和真实结果的偏离程度，刻画了学习算法本身的拟合能力。

方差度量了同样大小的训练集的变动所导致的学习性能的变化，刻画了数据扰动所造成的影响。

噪声表达了当前任务上任何学习算法所能达到的期望泛化误差下界，刻画了问题本身的难度。

偏差和方差一般称为bias和variance，一般训练程度越强，偏差越小，方差越大，泛化误差一般在中间有一个最小值。

如果偏差较大，方差较小，此时一般称为欠拟合，而偏差较小，方差较大称为过拟合。

一般来说，方差和偏差是冲突的，这称为偏差-方差窘境（bias-variance dilemma）。泛化误差与偏差、方差的关系示意图如下：

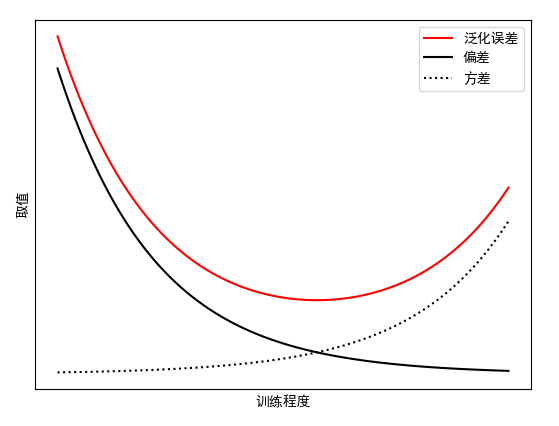
在训练不足时，学习器的拟合能力不够强，训练数据的扰动不足以使学习器产生显著变化，此时偏差主导了泛化错误率；随着训练程度的加深，学习器的拟合能力逐渐增强，训练数据发生的扰动渐渐能被学习器学到，方差逐渐主导了泛化错误率；在训练程度充足后，学习器的拟合能力已非常强，训练数据发生轻微扰动都能导致学习器发生显著变化，若训练数据自身的、非全局的特性被学习器学到了，则将发生过拟合。