类别不平衡

是指分类任务中不同类别的训练样本数目差别很大的情况。

需注意的是：类别不平衡学习中通常是较小类的代价更高，否则无需特殊处理。一般情况下，正例样本较少，反例样本较多。

基本策略—-再缩放：

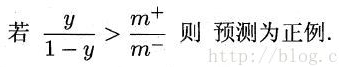以线性分类器为例，使用 y=w^{T}x+b对新样本x进行分类时，事实上是用预测值与阈值比较，通常y>0.5判为正例，否则反例。y实际上表达的是正例的可能性，几率y/(1-y)则反映了正例与反例可能性之比。若阈值为0.5，表明分类器认为正反例的可能性相同，即： 当正反例数目不同时，令m+表示正例，m-表示反例，则观测几率是m+/m-，因此判断规则应如下： 但分类器的决策规则是按公式1进行的，所以要对预测值进行调整：

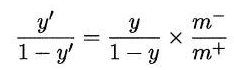
再缩放的思想简单，但实际操作却不平凡。一般是基于原始数据集进行训练学习，当用训练好的分类器预测时，将上述调整策略嵌入到决策过程中，称为“阈值移动”。

上采样

对正例(数目少)进行上采样，或者叫“过采样”，即增加一些正例，使两类数目接近。(对于图像，很多采样对样本做augmentation)

代表算法：SMOTE

步骤如下：

1. 对于少数类中每一个样本x，以欧氏距离(特征向量)为标准，计算它到少数类样本集Smin中所有样本的距离，得到其K近邻。

2. 根据样本不平衡比例设置一个采样倍率N，对于每一个少数类样本x，从其K近邻中随机选择若干个样本，假设选择的近邻为xn。

3. 对于每一个随机选出的近邻xn，分别于原样本按以下公式构建新样本。

   Xnew = x + rand(0,1) × norm(x-xn)

下采样

一般对反例(数目多)进行下采样，也叫“欠采样”，即去除一些反例的样本，使两类数目接近。

代表算法：EasyEnsemble(一种集成学习机制)

算法思想见网页，同时该网页文章中还介绍了很多其他过/欠采样的算法。

修改损失函数

1. 最简单的-加权

   以二分类为例,如果你的样本中0 label 特别多,而1 label 很少，这样会导致模型最后将所有样本预测为0，以保证整体 loss 最小。

   为了 解决这个问题，在 loss 上加权：

   loss = count1 / (count1 + count0) × loss0 + count0/ (count1 + count0) × loss1

   上式中 loss1表示 label1 的样本产生的 loss，loss0 同理。

   这样最终的 loss 会 balance 掉样本不均带来的 bias。

2. Focal Loss

   这是何恺明大神针对类别不平衡问题的发表的论文，详情请见原文。也可以借鉴知乎评论如何评价Kaiming的Focal Loss for Dense Object Detection？，加深理解。

这篇博客中提供了包含上述两种的多种loss的对比，以及代码实现，有需要的可以借鉴。